2019年北京高考数学考前复习策略指导

　　高考即将来临，考前十几天是数学冲刺的黄金时期，除了保持好的心态，高效全面的复习对于每位考生至关重要。那么如何有效利用时间，把高中数学众多概念、典型题、错题复习一遍，直击各个模块的解题策略和命题热点必不可少。下面我将从专业的角度，为考生指出高频考点命题方向，帮助考生高效备考。

　　高考数学分为两大板块：选择填空板块和解答题板块

　　一、选择填空板块

　　"得选填者得天下"。选择填空分值比较大，尽量保证60分以上。

　　选择题属于"小灵通"题，基本策略是：充分利用题干和选项两方面的条件所提供的信息作出判断，先特殊后推理，先排除后求解；而填空题是不要求写出计算或推理过程，只需要将结论直接写出的"求解题"。解答选填类题目的方法一般有直接法、特例法、数形结合法、构造法、排除法等．

　　1.集合运算

　　[解题策略]属于简单题，主要考查交并补运算。根据集合中元素的性质化简集合．注意表示元素，求解过程中不要忘函数定义域。

　

　　2.复数

　　[解题策略]主要考查复数的基本概念、几何意义、四则运算、复数的模，知道纯虚数的限制条件；虚部是i前面的数，i是虚数单位。属于简单题。

　

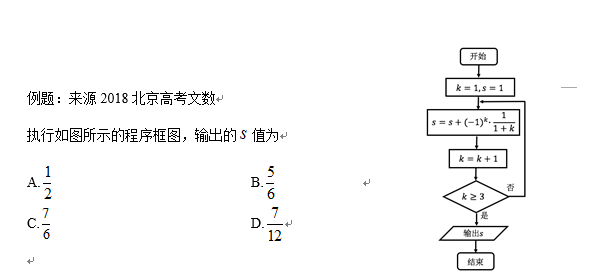
　　3.程序框图

　　[解题策略]属于简单题，要注意在哪一步结束循环；注意探究框图的功能。

　

　　4.线性规划

　　[解题策略]一般考查可行域的截距、斜率和距离三类问题问题；难度加大可能会考查动直线参数范围，结合最值问题，找临界值。

　

　　5.常用逻辑用语

　　[解题策略]主要考查充要条件，若p？q，则p是q的充分条件(或q是p的必要条件)；若p？q且q？/p，则p是q的充分不必要条件。数列、三角函数、平面向量等概念不要有知识盲区。全称与存在量词也是高频考点。

　

　　6.三视图

　　[解题策略]通过三视图先判断是柱体、椎体还是组合体，可以合理借助正方体和长方体还原立体图形，从而求出体积或表面积。

　

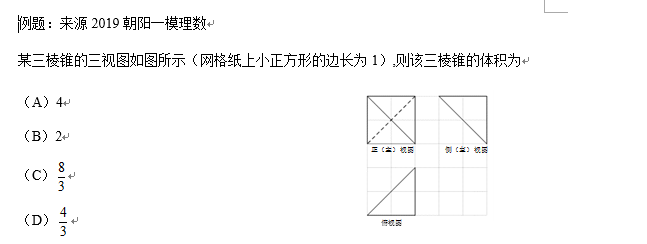
　　解读：如果立体图形还原不是常规的视角，可以先判定几何体形状，找准底和高求体积，锥体体积要乘三分之一。

　　7.数列

　　[解题策略]高考高频考点，熟练掌握等差数列、等比数列的性质及基本量的计算方法；

　　求Sn取得最值时，找到异号相邻项；由an与Sn的关系求通项时，要注意n＝1和n≥2的讨论。

　

　　8.平面向量

　　[解题策略]主要考查线性运算和坐标运算，特殊图形优选建系，普通图形也可以特殊化，通过建系解决；绝对值平方后记得开方。

　

　　解读：本题几何法解题较快，先通过平面向量求出表示区域为圆环，再求面积，注意平面向量与其他模块知识综合考查。

　　9.基本初等函数

　　[解题策略]一般北京高考考查指数函数、对数函数以及幂函数比较大小，注意化成同底或同指数，可以用单调性比较；指数函数与对数函数运算法则及性质。

　

　　解读：考题中新出现含参数的比较大小，可以把参数具体化，代值运算即可。

　　10.三角函数

　　[解题策略]通过二倍角公式及和差公式进行化简，引入辅助角合一变形，从而研究三角函数的定义域值域和性质--单调性、奇偶性、周期性、对称性。注意题干的转化。

　　

　　11.解析几何

　　[解题策略]⑴直线与圆要注意圆方程的标准形式和一般式，通过圆心到直线的距离与圆半径的大小关系判定直线与圆位置关系，通过两圆心的距离与两半径比较从而判断圆与圆位置关系；⑵注意判定圆上的点到直线距离最大值与最小值问题，先求圆心到直线的距离，再加减半径；⑶熟练运用椭圆、双曲线与抛物线的定义，掌握a、b、c及离心率e基本量运算方法。

　

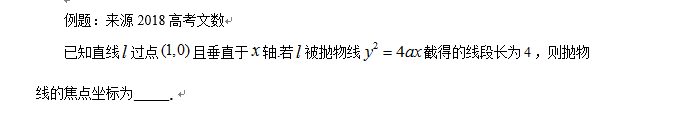
　　12.函数综合

　　[解题策略]已知函数的解析式，判断其图象的关键是由函数解析式明确函数的定义域、值域、单调性、奇偶性、周期性等，根据这些性质对函数图象进行具体解析判断；如果涉及分段函数含参问题，可以数形结合、分类讨论。

　

　　解读：从今年模考题来看，容易出"满足条件"的开放题，实则要找全题干信息，分析函数性质，反复检验答案是否合理。

　　13.数学文化

　　[解题策略]需要认真解读题干，按照题意结合数论知识综合推理论证，可以列表或画图，选用合适的方法。

　

　　14.极坐标与参数方程（理科）

　　[解题策略]需要掌握极坐标系与平面直角坐标系的转化法则，学会通过参数建立方程关系从而求解。

　

　　二、解答题

　　北京高考考查6道大题。分别是三角函数（解三角形）、立体几何、概率统计、数列、导数、圆锥曲线。文理科考查区别比较明显，下面分别进行分析。

　　一、理科四道大题（圆锥曲线和导数放在最后一起）

　　1.三角函数与解三角形

　　[命题方向]

　　北京高考理科一般考查解三角形较多，也会有三角函数考查。尤其作为解答题，更可作为"头号"热点对待。三角函数主要考查诱导公式、和差角、二倍角、辅助角公式；解三角形主要指利用正、余弦定理，三角形的面积公式等解决已知三角形的求角或边的问题．解答题考查的位置、形式更为固定，但难度一般．

　

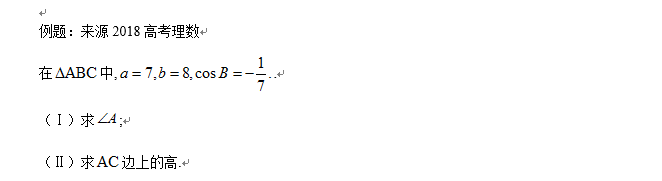
　　2.概率统计

　　[命题方向]

　　高考对理科统计概率考查主要体现在以下几点：

　　(1)运用频率分布直方图求解参数和各组样本容量，注意纵轴的值是频率除以组距；

　　(2)会求平均数、众数、方差，了解其性质；注意题干要求，求平均数取中间值还是两端数值；

　　(3)准确判断超几何分布和二项分布，先设事件，再求概率，最后列分布列。

　

　　3.立体几何

　　[命题方向]

　　高考对理科立体几何主要考查空间向量，虽然前两问同文科一样，但是时间不充裕的学生建议直接建系，要注意计算准确；求解二面角时要注意锐角还是钝角；直线与平面夹角求解注意正余弦转化。本题计算量较大，注意把控时间。

　

　　解读：第三问要回答是或否，然后设，从而解出Q点坐标，通过平面与平面法向量垂直，看是否可以求出值。

　　4.数列综合

　　[命题方向]

　　本题在高考中难度最高，建议一模二模成绩在125分以下学生只做第一问，放弃二三问为其他题赢得时间；125分以上的学生在有充足时间的基础上可以尝试做二三问，一定要认真仔细读题，获取有效信息，合理运用反证法等进行推理证明。

　　

　　二、文科前四道大题

　　1.三角函数

　　[命题方向]

　　高考文科考查三角函数的概率高于解三角形，主要体现在两个方面：

　　(1)考查图象的变换和作图，主要是参数A，ω，φ的变化对函数y＝Asin(ωx＋φ)的图象的影响．作图主要考查五点作图法以及参数A，ω，φ值的确定．

　　(2)三角函数的性质包括周期性、奇偶性、单调性等问题，解题思路是先化为一个角的三角函数，然后再利用三角函数的性质求解，主要考查学生综合运用所学知识解决问题的能力。

　

　　2.数列

　　[命题方向]

　　文科数列相对来说难度不高，是大题比较容易得分的，考查主要考查以下几点：

　　(1)等差数列和等比数列的定义和性质；非等差等比数列求通项。

　　(2)熟练掌握等差数列和等比数列的求和公式，会分组求和，错位相减和列项相消一般不考。与函数性质相结合要会转化，比如18年高考题。

　

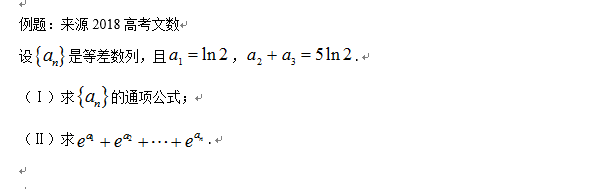
　　3.概率统计

　　[命题方向]

　　高考对文科统计概率考查难度不高，通过有效审题，列举出符合题意的情况，再求概率即可。注意频率分布直方图求解参数和各组样本容量时，纵轴的值是频率除以组距；会求平均数、众数、方差，了解其性质；注意题干要求，求平均数取中间值还是两端数值，方差越小越稳定。

　

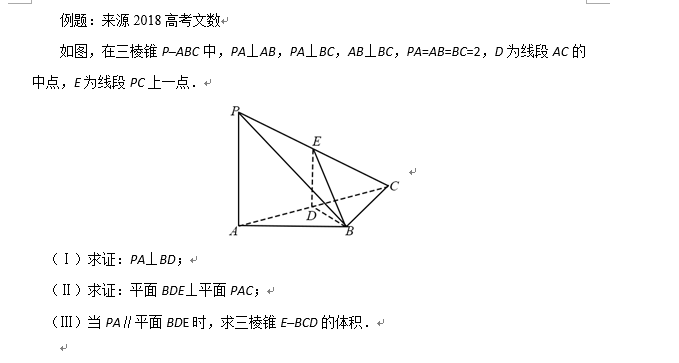
　　4.立体几何

　　[命题方向]

　　高考对文科立体几何考查主要体现在以下几点：

　　(1)熟练掌握空间中直线与平面平行与垂直的判定定理及性质；证明线线垂直和面面垂直都需要先证明线面垂直；

　　(2)第三问一般会考查体积或动点问题，体积换底是常用的方法。动点问题抓住特殊点和做垂直。

　

　　文科理科解析几何综合

　　[命题方向]

　　高考对文科理科考查相差不大，重难点主要体现在以下几点：

　　⑴明确是双动点问题还是单动点问题，双动点问题需要设直线联立求韦达定理，单动点问题先设点，用该点表示其他点，最后通过椭圆方程回代求解；注意有时单动点问题也要设直线；

　　⑵难题需要思考几何关系转化，包括利用几何图形结构特征转化垂直和平行关系。

　　⑶对于弦长面积类问题要记住弦长公式，定值定点问题可以先找斜率不存在和等于0的特殊情况。

　

　　解读：本题比较常规，直线与椭圆相交问题要考虑斜率是否存在；若斜率存在，联立求韦达后记得，可能由此得出参数范围；求最值问题，优先考虑二次函数和均值不等式。注意有时候第一问就联立直线与椭圆方程也是可能的，例如西城二模的相切问题，通过求出参数，从而得到椭圆方程。

　　文科理科导数综合

　　[命题方向]

　　高考对文理科导数考查相差不大，理科考查复合函数求导，文科不做考查。

　　⑴第一问以往通过导数几何意义求切线方程，注意过某点切线方程求法；也有可能直接求单调区间和极值；

　　⑵导数的应用，包括单调区间、极值最值、零点问题、不等式问题、恒成立与存在性问题、渐近线、设而不求等；

　　⑶求完导数最高次项系数含参数要讨论正负和零，通过导函数正负判断原函数增减，建议在草纸上画图，答题纸上画表格；

　　⑷不等式问题可以构造新函数，再求导，研究单调区间等；

　　⑸恒成立与存在性问题弄清楚要求函数最大值还是最小值；

　　⑹二次求导要思路清晰，时刻谨记"导函数的正负判断原函数的增减"，找到对应的原函数；

　　⑺虚设零点也要关注，注意虚设零点的目的是什么，注意计算中的代换关系；

　　⑻如果题目已知极值点求参数，求完要带回原函数求单调区间，注意导函数等于0不一定就是极值点，务必用单调性检验。

　　

　　解读：从今年模考题看出，二次求导依然是热门考点，通过二次导求出一次导函数增减从而判定正负，再判断原函数增减。建议在草纸上把一次导和二次导的过程拆分写，这样不容易混淆，保持思路清晰，明确知道自己要的结论；如果涉及虚设零点，可以通过导函数等于0进行整体代换。

　　圆锥曲线和导数合理安排时间，在确保第一问正确的情况下尽可能的把后面的问题做全，思路清晰的分析问题，选取合适的方法。

　　希望广大考生控制好选填和前三道大题时间，稳扎稳打，在规定的时间拿到理想的分数。最后祝大家考试顺利，金榜题名！

        了解更多关于学习咨询，请关注“北京新东方学校中小学1对1网站”，更多精彩等您发现！

责任编辑：刘汉甜

• 北京新东方学校2021财年经营管理…
• 2021年各高校新增37个本科专业
• 中考前最后1个月该怎么安排？
• 北京教育考试院：2021年北京中考…
• 2021年北京中考加分细则发布
• 高考推荐篇目导读之《平凡的世界…
• 师范大学怎么选，这三类大学值得…
• 清华北大30名学子参军入伍，奔赴…
• 2021年北京高校将增加这些新专业…
• 2021校友会中国大学排名出炉

① 凡本网注明“稿件来源：北京新东方学校”的所有文字、图片和音视频稿件，版权均属北京市海淀区私立新东方学校所有，转载请注明“来源：北京新东方学校”。
② 本网未注明“稿件来源：北京新东方学校”的文/图等稿件均为转载稿，本网转载仅基于传递更多信息之目的，并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用，需自负版权等法律责任。如擅自篡改为“稿件来源：北京新东方学校”，本网将依法追究法律责任。
③ 如有本网转载稿涉及版权等问题，请作者见稿后速来电与北京新东方网联系，电话：010-62578989。