一、排列组合在GRE Quantitative Reasoning中的定位

　　根据学员及我的多次考试经验，排列组合在考试中的题目并不多，甚至有时可能不出，所以建议“之前没学过”且“备考时间非常短”的学员“考虑”扔掉，把精力放到其他考点的复习和练习上。

　　二、乘法原理及排列

　　(multiplication principle)(permutations)

　　1. 假如一个人从A点到B点，有2条路线，B到C点有3条路线，那么这个人从A经过B到达C点共计路线数量为：2*3=6条

　　2. 假如，早晨起床我们有4件上衣可以选，3条裤子可以选，2双鞋可以选，（暂不考虑颜色等搭配不当的问题）则有4*3*2=24种不同的穿法

　　3. 再假如，由0-9这10个数字构成一位3位数的密码锁密码，第一个位置有10种选择方式，第二个和第三个位置也分别有10种选法，则共计可以有10*10*10=1000种不同的构成方式，而假如要求构成的密码锁不能使用相同数字(repetitions are not allowed in the code)，则有10*9*8=720种

　　那么：如果有5个人排成一排，有多少种不同的站位顺序呢(arrangements)？

　　同理：第一位置有5个人可以站，第二个位置有剩下4个人可以，以此类推，所以共计有5*4*3*2*1=120种不同的排列方式，也就是5!(5 factorial，中文读作“5的阶乘”)。

　　同理：3个人的排序方式为3!=3*2*1=6种

　　阶乘的运算也完全有可能直接出现在考试的运算题中：

　　Example 1: (21!-20!)/(20!-19!)=?

　　而假如，要求只从这5个人中挑选3个人坐在座位上，有多少种不同的排序方式呢？

　　我们的列式将是5*4*3，而这个式子可以演变成5*4*3*2*1/2*1=5!/2!=5!/(5-3)!，这是排列公式的“诞生”过程。我们定义5P3()表示：“从5个不同的元素中任取3个不同元素，有多少种不同的排序方式”，公式就是上面的5P3=5!/(5-3)!

　　同理8P2=8!/(8-2)!

　　由此得到：mPn=m!/(m-n)!

　　不过这里需要注意的是，如果题目的要求是从8个人中选2个人，有多少种不同的排序方式，我们直接按照初始的思考方式，使用8*7=56会更方便，我一般不会写8P2=8!/(8-2)!=8*7=56，因为这样相当于增添了两个环节，对于考试时间很有限的我们，直接写8*7会更高效。不过仍建议掌握公式，因为有些题目可能因为运算结果较大，选项会直接写成带有阶乘的表达方式，那么此时我就会选用带有阶乘的公式了。

　　所以两种方式都要掌握，根据题目情况，择优选取。

　　三、组合(combinations)

　　假如有5本书，要求选取2本书，有多少种不同的选取方式(selections)？

　　我们仍然可以考虑有两个位置，第一个位置有5种放法，第二个位置有4种放法，而如果直接用5*4，就会出现重复问题。因为我放过AB，也放过BA，因此需要再除以2。

　　如果是取3本书呢？使用5*4*3就会出现ABC, ACB, BAC, BCA, CAB, CBA六种重复，也就是3!。所以5选3，我们就可以表示成5C3＝5*4*3/3*2*1，同理9选4，我们可以表示成9C4 =(9*8*7*6)/(4*3*2*1)=( 5P4)/(4!)=(9!)/(9-4)!(4!)

　　因此：mCn=m!/(m-n)!n!

　　另外，通过公式我们可以得知：mCn = mC(m-n)

　　这个也不难理解，假如你从5本书中每选3本，就会有2本剩下，有多少个3，就有多少个2。

　　特别的：

　　mPm =m!

　　mCm = mC0 =1

　　mP1= mC1 =m

　　规定0!=1

　　官方特别写法：

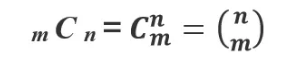
　　四、关于排列组合的选用

　　简单的说，就是：“有序用排列，无序用组合”。

　　排列的例子：

　　1. 排队问题

　　2. 坐座位问题

　　3. 数位问题

　　组合的例子：

　　1. 选人问题

　　2. 选书问题

　　3. 连线问题

　　还可以通过“如果选取元素的顺序发生变化，是否就会形成新的结果”来判断，如握手问题，“我和你握”跟“你和我握”是一样的，那就是无序，需要使用组合计算，“我坐在你左边”跟“我坐在你右边”是不一样的，那就是有序，需要使用排列计算。

　　五、关于运算符号的选用

　　我们说：“分步用乘法，分类用加法”。

　　比如“乘法原理”的例子1，从A经过B到C有2*3=6种路线，如果从A到另外一点D有2种路线，D到达C有2种路线，那么A经过D到达C就有2*2=4种路线，最终从A经过B或D到达C，共计就有6+4=10种路线。

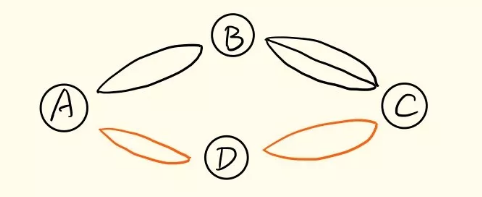
　　再比如：我有4件上衣可以选，3条短裤或者2条长裤可以选，2双鞋可以选，那么穿短裤的搭配方式就是4*3*2，穿长裤的搭配方式就是4*2*2，所以我有共计4*3*2+4*2*2=40种穿搭方式（当然如果可以某部分不穿或者可以穿多件的话总的穿搭方式就会更多……）。

　　六、常见考试题型：

　　1. 乘法原理的直接使用

　　Exercise 1

　　180=(2^2)(3^2)5, how many positive factors does 180 have?（鸡精题）

　　2. 捆绑法

　　Exercise 2

　　ABCD四本书横着放在书架上，要求AB两本书必须挨在一起，有多少种不同的arrangements?（鸡精题）

　　3. 分组排列或抽选

　　Exercise 3

　　A reading list for a humanities course consists of 10 books, of which 4 are biographies and the rest are novels. Each student is required to read a selection of 4 books from the list, including 2 or more biographies. How many selections of 4 books satisfy the requirements?（OG题）

　　Exercise 4

　　一对父母带着4个孩子看电影，父母2人必须坐正中间，孩子做两边，how many different arrangements are possible?（鸡精题）?

　　4. 穷举法

　　原则上这些题都可以使用穷举法，不过有些情况较多，不建议使用，而类似于练习1和2可以使用。

　　5. 顺序讨论法

　　Exercise 5

　　How many 3-digit positive integers are odd and do not contain the digit 5??（OG题）

　　6. 结合概率题进行考察

　　Exercise 6

　　Eight points are equally spaced on a circle. If 4 of the 8 points are to be chosen at random, what is the probability that a quadrilateral having the 4 points chosen as vertices will be a square??（OG题）

　　答案

　　Example 1: 400/19

　　Exercise 1: 18

　　Exercise 2: 12

　　Exercise 3: 115

　　Exercise 4: 48

　　Exercise 5: 288

　　Exercise 6: 1/35

　　解析

　　简单解析：

　　Example 1: 提取公因数进行约分运算

　　Exercise 1: prime factor 2 has 3 different selections, 不取；取1个；取2个，同理，3 has 3 different selections and 5 has 2 selections, 然后再利用“乘法原理”3*3*2=18个（注：都不取的时候乘得1，都取的时候乘得180本身）

　　Exercise 2: 把AB当做一个整体，也就是先按照3个整体进行排序，再考虑AB内部顺序，所以(3P3)( 2P2)=3!*2!=12

　　Exercise 3: 分类讨论，4选2，6选2；4选3，6选1；4选4

　　所以

　　Exercise 4: 排父母，排孩子，不用两组进行再排序。

　　所以(2P2)( 4P4)

　　Exercise 5: 奇数且不能有数位5，则先考虑最后一位，有5-1=4种放法，再考虑第一位置不能为0，有10-1-1=8种，中间数位无要求，有10-1=9种，所以4*8*9=288

　　Exercise 6: 满足题意的正方形共计2个，所以分子为2，8个点任取4个，所以分母为=70，所以概率为2/70=1/35

新东方版权所有，转载请注明来源：新东方国际教育北京学校http://bj.xdf.cn

（责任编辑：admin）

姓 名：

电 话：

我接受并同意《用户服务条款》和《隐私权相关政策》

免费预约