近日，IBO 完成了针对 2019 至 2028 年 IB 数学方向的考纲修订，并于 2019 年 秋季开始正式实行。为了培养学生批判性思维方式，以及满足学生日益多样化的 需求，IB Group5 数学方向的课程在现有 Mathematical Studies Standard

　　Level（简称 MSS）， Mathematics SL ， Mathematics HL 及 Mathematics

　　Further Study ( 简 称 MFS) 基 础 上 ， 新 加 入 Application and

　　Interpretation( 简称 Application) 和 Analysis and Approaches （ 简 称 Analysis）两门科目供学生选择。新增的这两门课和已有的数学科目有什么异同？ 大学到底认不认？本文将逐一进行详细的解答。

　　一、什么是 Application？

　　全称，Application and Interpretation：重应用，偏统计

　　根据 IBO 的描述，Application 为用数学思维来描述现实世界问题，和解决实 际问题的学生而设计，启发学生利用科技的力量，探索数学模型，享受用数学来 解决实际问题的过程。Application 在课程设计上着重在启发学生用数学知识解 决实际问题，所以在教材授课过程中会将数学知识和统计知识相结合。SL 课程设置与 Mathematics SL 基本相同，但在 HL 的课程中加入了大量的统计学知识。

　　从 Oxford 出版的 Application HL 课程设计上看（如上图），课程讲解从数据的 收集和描述开始，到概率和统计，随后引入微积分的知识，最后讲解数据的处理 和分布（ Chi-Squared Test，Hypothesis Test， Confidence Interval／Level) 的有关知识，并在课本最终章涉及到一部分图论的内容，最小旋转树的构建，并 对算法方向两大经典问题（Chinese Postman Problem， Traveling Salesman Problem)进行学习。

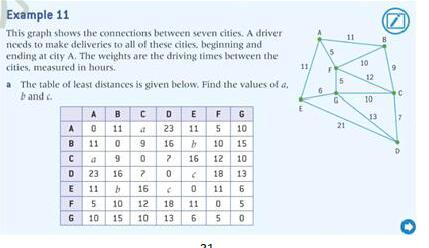
　　以选自 Oxford 教材 15.5 一道例题来说，在如上所示的的图中，点代表司机要 到访的城市，线代表了各城市之间的车程时长，一位销售员从 A 城市出发，要 经过图上的所有城市。（a）.根据图的信息，把表格中数据补充完整。这道问题 对大多数同学都没太大难度，我们只需要用横纵坐标确定两座城市，找到两点之 间的最短路径即可，如 a 所代表的就是 A 点和 C 点之间的时长，从 A 点到 C 点 没有直达的路，但可以走 AFC 17 个小时，或者 ABC 20 个小时等路线，其中最 小值为 17，所以 a 的值就是 17 了。而对于第二个问题，求司机从 A 点出发的 最短距离及生成最短距离的路线，这就是一道典型的 Traveling Salesman Problem，对于没有学习过的同学们就会有些难度了。一般的同学遇到这样的问 题，会采取列举的方法，把从 A 出发可能的行驶路线全部列举出来，但是，我 们这道题目中有 7 个城市，从 A 点出发再回到 A 点的路线有 6!/2 = 360 种， 想要完全列举出来基本不可能。这个时候我们就要用到在统计学中常用的一种 思考方式，能不能把我们这个复杂大问题拆分成若干个相对轻松些的小问题，再 逐一攻克这些简单的小问题从而解决大问题呢？ 这种思维方式常用于解决应 用数学，计算机，运筹学等学科的问题。而我们这道题要用到正是应用数学中 nearest neighbor algorithm （近邻算法）来解这道题，也就是我们从 A 点出 发，选择离 A 点处最近的，未到访过的邻居城市为第二个要拜访的城市。从 A点出发最近没有到访过的城市是 F，需要的时长是 5。来到 F 后，再在所有未拜访过的城市中选择一个最近的城市，如此循环迭代，从而确保了我们在每一个城 市所做的决定都是当下的最优解。整合所有小的最优解，就可得出整个大图的最优解了。

　　二、什么是 Analysis？

　　Analysis and Approaches：重论证，专业性强，难度高

　　Analysis and Approaches 为有计划在大学期间学习数学专业或者想选择需要 较强数学基本功的专业（如物理学，天文学，计算机等专业）的同学设计。在 Analysis 课 程 中 ， 学 生 要 学 习 如 何 建 立 严 谨 的 数 学 论 证 （ rigorous mathematical arguments)， 并且解决实际和抽象的问题，重在较学生从论证 的角度解决数学问题，增强学生们的数学分析能力和数学思维能力。Analysis 在 课程设置上和大学数学中的数学分析联系紧密，整体知识覆盖面广，难度偏难， 但对学生思维方式的启发非常有帮助。

　　Analysis 主要包括 algebra，functions，geometry，statistics，calculus 五大 章，前五章在 SAT2 中都有涉及，但是讲解比 SAT2 更加细致，对学生的要求也 更高。

　　SL 难度相当于在 SAT2 的基础上加入了 AP 微积分 AB 中微分（求导）的知识， 但不涉及微积分 BC 积分部分。HL 目前市面上暂时没有看到教材，但从考纲上 看，Calculus 部分难度与微积分基本持平。但是，analysis HL 在其余四章中涉 及知识点更加琐碎。其中 HL 最大的特点是引入了数学归纳法和反证法的介绍。 数学归纳法的中心思想是要首先证明命题在某个起始点成立，然后假设命题在任意值 n 时成立，证明从任意值（n）到下一值(n+1)的过程有效，产生类似“多米诺骨牌”的效应，从而推导出命题在任意值都成立。比如大家熟悉的高斯算法

　　求从 1 加到 n 的算术和 1 + 2 + 3 + 4+. . . . . +? = ??(?+1)都知道这个结果。我们是产生的原理，最后一项 n 加上第一项 1，组成一组和为 n+1 的数据，而在这? ??(?+1)个数列中，有 个和为 n+1 的数组，所以所有数据加起来的和就是。
　　原理

　　看起来是没有问题的，但是要如何保证这个公式对任意一个正整数 n 都能适用呢？这就需要严格的数学证明。对这个问题的证明中，我们就可以采用数学归纳法了。首先我们验证在 n=1 时，公式是否成立。很显然，1 = 1?2式成立。

　　假设在任意整数 n 时，1 + 2 + 3 + 4+. . . . . +? = ??(?+1)测试一下当有 n+1成立，

　　个数相加时，该公式是否仍成立，也是就是 1 + 2+. . . . +? + (? + 1) =(?+1)[(?+1)+1]是否仍成立。通过我的假设可以得出 LHS=??(?+1)+ ? + 1 = (? +1) ? (? + 1) =RHS，成立，所以该公式在任意正整数 n 成立的时候，我都能得到公式在 n+1 时也成立。在论证一开始我们就有提到，公式在 n=1 时成立，从而也以推出公式在 n=2 时也成立，如此循坏递推下去，我们就可以得到公式对于 任意正整数 n 都成立。数学归纳法在许多数学原理和推论的论证中都有体现， 同学们会在 analysisHL 的学习中对此有更深的认识。

　　随着科学技术的发展，一部分传统技能开始变得多余，并有逐步被科技所取代的 趋势。招生官们在录取时也越来越青睐那些更有“创造力”的申请人，哪怕这些 学生在标准化考试中可能略有不足。为顺应此趋势，IBO 这次课程改革更加注重 对学生批判性思维（critical thinking）的培养。而批判性思维就要求学生不仅 学会一个知识，并且可以把所学知识拓展到生活或者其他领域中去运用。在数学 的教学中就要求学生可以识别所学知识可以应用的环境，构建逻辑论证体系及 风险意识，理解数学知识和科技发展的相关性并能够讲数学方法应用到熟悉与 不熟悉的情景。这都是现阶段大学申请以及未来工作岗位中愈加重要和抢手的 技能。

　　从整体教学思路上来说，新加入的两门数学科目（Application 和 analysis）较 之前传统高中数学教学有着较大的突破。在高中阶段引入数学论证及算法应用 等内容，在现在所有的高中教学体系（包括美高）内实属少见。Application 和 Analysis 两科在 HL 阶段的设计更贴近于大学教学体系，内容复杂，难度偏高，但会对未来理科或者工科的学习非常有帮助。

　　三、IB 数学应该怎么选？

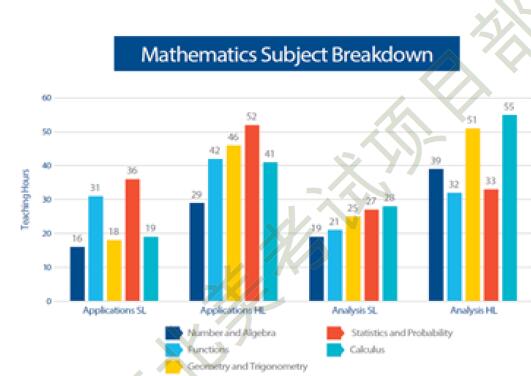
　　通过 IBO 官方对个知识点教学时长的对比（见上图）我们可以发现，Analysis SL 在各科目分配上基本平均，与现有的 Mathematics SL 相似；Application SL 更强调统计和函数的教学，弱化了微积分的教学，难度相较于其他两科有所降低。 Analysis SL，Application SL，Mathematics SL 更适合数学功底较弱，未来打算选择文科，商科偏文科，或者艺术专业学生选择。Mathematics HL 知识覆盖面较广，适合未来想选择理工科方向专业，但又不确定具体专业的同学。Analysis HL 重点培养学生的论证能力，推荐未来打算学习纯数学，物理学等纯科学类理 科的同学选择。Application HL 重点培养数学应用能力，更适合有意应用数学， 计算机，运筹学，工程设计学等应用类理工科的同学选择。

　　四、主流考试数学知识点对比

　　由于 SAT1 和 ACT 数学考点很基础，不在本文讨论之列。和其他数学相关的专 业对比来说，SAT2 的数学相对基础，AP 微积分只涉及和微积分相关的知识， 但 IB 数学涉及的知识面就会更广一些，但若想对于某个知识点进行具体学习， 就要进行 Further Study 的学习。

　　下面的表格展示了各学科涉及的重点章节的对比：

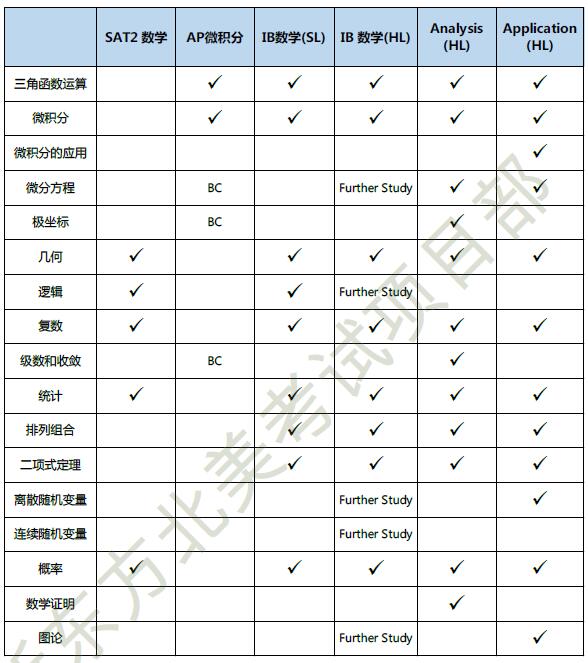
　　注：

　　1.该表格仅对部分章节进行比较，并不是所有内容。

　　2. 有些章节尽管有所涉及，但要求学生掌握程度不一样，望读者注意区分。

　　五、部分世界名校对于新科目的跟进

　　一些知名大学录取政策也根据 IB 课程调整进行了相应的调整，英国及加拿大部 分大学对 2019 年及以后参加 IB 课程系统的申请者已经提出了具体科目上的要 求。LSE（伦敦政治经济学院）为例，LSE 的数学，经济学 和金融数学三个专业， 只接受 analysis and approaches HL 成绩。经济学，金融学，精算学，计量经济学和数理经济学，商科统计学，经济史可接受任意一门成绩，但是更推荐Analysis and Approaches HL。而其他与数学相结合的专业，如地理经济学， 环境政策与经济，管理学，哲学与经济等专业，可接受任意一门课程的成绩。多 伦多大学可接受 Application HL，Analysis SL 或 Analysis HL 作为微积分的 预修课，但对于 Application SL，需要进一步和学校沟通之后再决定。

　　六、总结

　　综合各学校要求分析发现，Analysis 适用的学科范围更广，相对来说是一个更 加稳妥的选择。但 Analysis HL 课程难度偏高，数学功底较扎实的同学或未来有 意向从事理论研究的同学，而 Application HL 适合对数学与生活有着更好理解 的同学。希望同学们可以根据自己未来的专业定位，选择适合自己的课程。

　　教材参考：

　　Mathematics: Applications and Interpretation (Higher Level). Oxford

　　University Press. 2019.

　　Mathematics: Applications and Interpretation (Standard Level). Oxford

　　University Press. 2019.

　　Mathematics: Analysis and Approaches (Standard Level). Oxford

　　University Press. 2019.

　　41

　　北京新东方学校北美考试项目部

　　Mathematics For the International Students. Mathematics HL (Core). Third Edition. Haese Mathematics.

　　Mathematics For the International Students. Mathematics SL (Core). Third

　　Edition. Haese Mathematics.

　　Barron's SAT Subject Test: Math Level 2. 10th Edition. Barron's AP Calculus(2010).

　　IBO: https://www.lmsd.org/uploaded/documents/Academics/IB/ib_mathema tics.pdf

　　http://blogs.ibo.org/blog/2017/05/15/what-does-the-mathematics- community-want-in-the-21st-century/

　　LSE: http://www.lse.ac.uk/Study-at-LSE/Undergraduate/Prospective- Students/How-to-Apply/Entry-Requirements

　　多伦多大学：

　　https://future.utoronto.ca/apply/requirements/international-

　　baccalaureate

（责任编辑：admin）

姓 名：

电 话：

我接受并同意《用户服务条款》和《隐私权相关政策》

免费预约